Projects

Bayesian Statistics

In this project for the course Bayesian Statistics by Prof. dr. Herbert Hoijtink, the main goal was to develop a Gibbs sampler for a Bayesian linear regression model. By using two simulated data set the Gibbs sampler was tested and the results were compared. The Gibbs sampler was then applied to a real data set to identify the key factors that play a role in the University admittance process, using a open source data set. We used non-informative conjugate priors, as specified in the info note underneath. Next to this Bayesian Model Averaging was used to identify the most important variables in the model. The project was rewarded a 10.0/10.0 grade. The project can be found here.

Note

Theorem
\(Y_i = b_0 + b_1x_{1i} + b_2x_{2i} + b_3x_{3i} + e_i\) with \(e_i\) i.i.d. \(\sim N(0,1/\tau)\) and priors
\(b_0 ... b_3 \sim N(0,1/\tau_b)\)
\(\tau \sim gamma(\alpha, \beta)\)

conditional distributions:
\(f(b_0|b_1,b_2,b_3,\tau,Y_1,...,Y_n) \sim N(\frac{\tau}{n\tau + \tau_b}\sum_{i=1}^n(Y_i -(b_1x_{1i} + b_2x_{2i} + b_3x_{3i}), \frac{1}{n\tau + \tau_b})\)
\(f(b_1|b_0,b_2,b_3,\tau,Y_1,...,Y_n) \sim N(\frac{\tau\sum_{i=1}^n(Y_i-(b_0 + b_2x_{2i} + b_3x_{3i})x_{1i})}{\tau\sum_{i=1}^n(x_i^2+\tau)}, \frac{1}{\tau\sum_{i=1}^nx_{1i}^2 + \tau_b})\)
...
\(f(\tau|b_0,b_1,b_2,b_3,Y_1,...,Y_n) \sim gamma(\alpha+n/2,\beta+\frac{1}{2}\sum_{i=1}^n(Y_i -(b_0 + b_1x_{1i} + b_2x_{2i} + b_3x_{3i})^2))\)

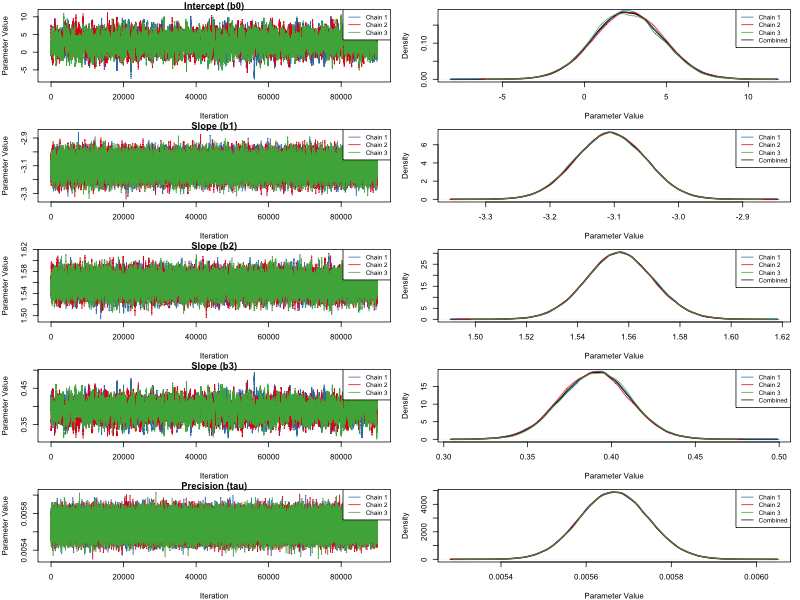Figure 1. MCMC sampler of related dataset

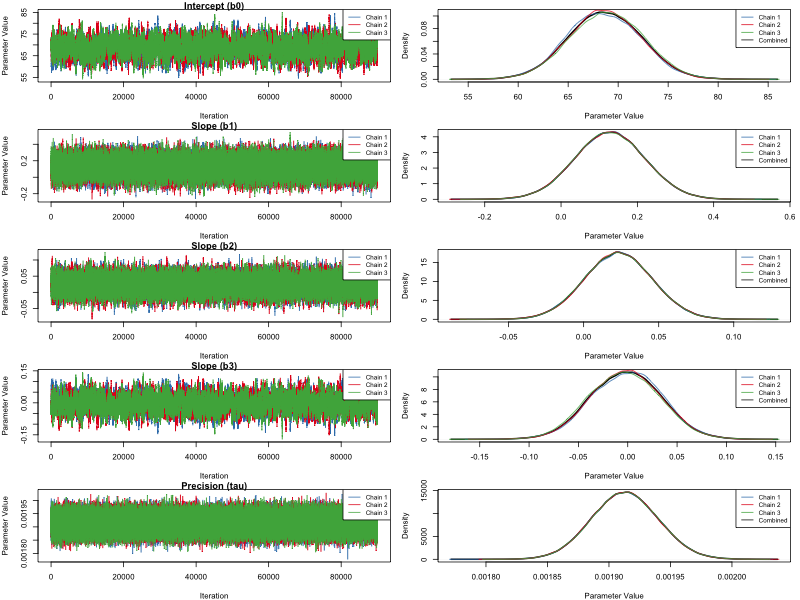Figure 2. MCMC sampler of unrelated dataset